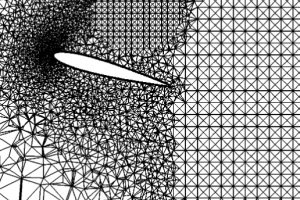
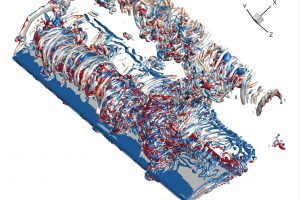
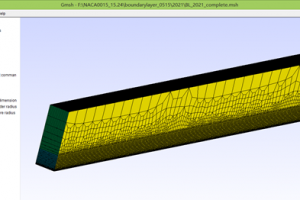
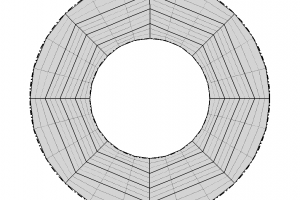
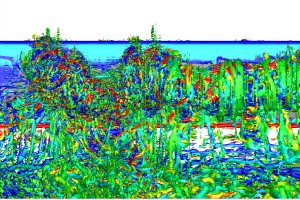
For complex geometries, we can use Solidworks to build the CAD model and use star-ccm+ for mesh generation. This blog gives a step-by-step instruction on the mesh generation of a round-tip wing.

DOI: 10.1017/jfm.2022.224
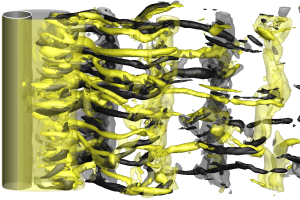
The vortex dynamics of leading-edge vortices on plunging high-aspect-ratio (AR = 10)
wings and airfoils were investigated by means of volumetric velocity measurements,
numerical simulations and stability analysis to understand the deformation of the
leading-edge vortex filament and spanwise instabilities.

Ansys ICEM CFD is a popular mesh generation software. In this blog, we show how to convert the mesh generated by ICEM to Nektar++ format.

In applications Pointwise (or the predecessor Gridgen) is a popular mesh generation software. In this post we go through the procedures to convert the linear mesh generated by Pointwise/Gridgen to arbitrary high order mesh for the solvers in Nektar++.

The visualisation of the flow fields output by Nektar++ may not look smooth if the resolution is not enough. A feasible solution is interpolating the spectral element field to a finite difference grid and then doing the post-processing using a Gaussian filter.

In this post, you will learn how to run an interactive job on ARCHER2 for postprocessing using Paraview.

by Hongyi Jiang (University of Western Australia)
DOI: 10.1063/5.0041168
Using Nektar++, we report a systematic numerical convergence study for the case of flow past a circular cylinder at Re = 3900.

The 5th annual Nektar++ Workshop will bring together developers and users of all experiences to hear about new and future developments in Nektar++ and the exciting science and engineering being undertaken with the code.

At our recent Nektar++ tutorial we produced a number of videos supporting the background of the framework. We include them here for general reference and also make the presentations available in Keynote and Powerpoint formats.

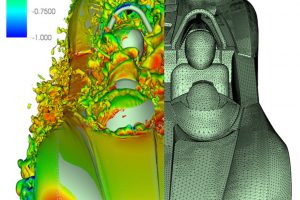
We present the successful deployment of high-fidelity Large-Eddy Simulation (LES) technologies based on spectral/hp element methods (SEM) to an industry-relevant configuration. The simulation is carried out on a real automotive car, namely the Elemental Rp1 model.