Jan 26, 2022
Ankang Gao
Community Blog
No comment

Post-processing flow fields in the finite-difference grid

The visualisation of the flow fields output by Nektar++ looks not smooth if the resolution is not enough.

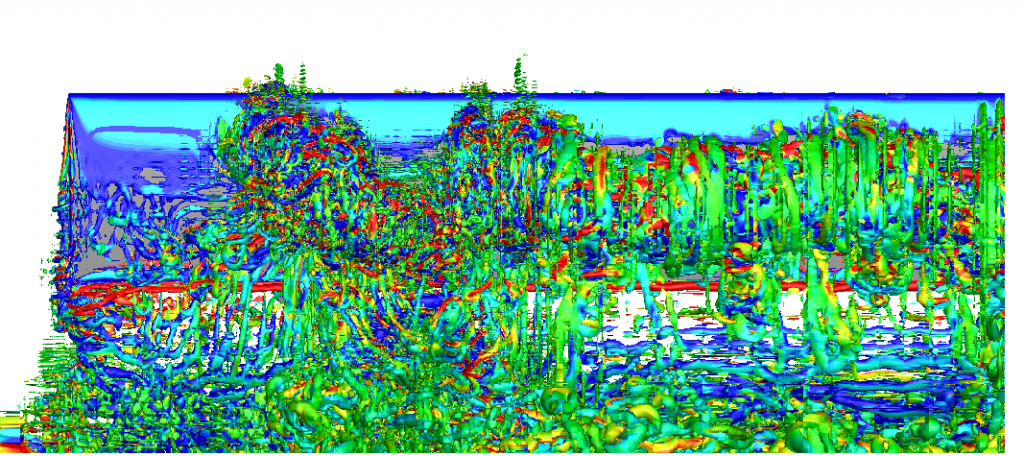
Figure 1 is an example of the leading-edge vortex generated by a plunging wing at Reynolds number 10,000. The result is from paper: Son, O., Gao, A., Gursul, I., Cantwell, C., Wang, Z., & Sherwin, S. (2022). Leading-edge vortex dynamics on plunging airfoils and wings. Journal of Fluid Mechanics, 940, A28. doi:10.1017/jfm.2022.224. Although there are 40M degrees of freedom for each velocity component, the discontinuities between element boundaries are still very obvious and the vortex looks not smooth.

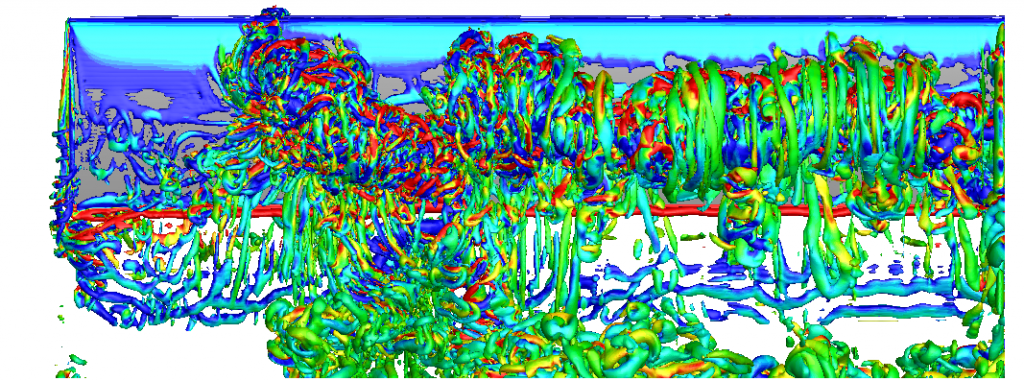
Figure 1. Q iso-surface coloured by the spanwise vorticity. Post-processed in Nektar++. (FieldConvert -m QCriterion -m vorticity)

A feasible solution is interpolating the spectral element field to a finite difference grid and then doing the post-processing using the finite difference method. In figure 2, the spectral element field is first interpolated into 301 x 301 x 601 grid in the domain [-0.5, 2.5] x [-0.5, 1.5] x [0, 5.5]. Then the vorticity and Q are calculated using a second-order central difference scheme. The Q iso-surface looks much smoother.

Figure 2. Q iso-surface coloured by the spanwise vorticity. Post-processed in a finite-difference grid

The bash script to do the interpolation is

for((n=64; n<=64; n+=1))
do
    mpirun -np 12 $NEKBIN/FieldConvert -f -e -v -m \            
        interppoints:fromxml=wing.xml:fromfld=wing_${n}.chk:box=301,301,601,-0.5,2.5,-0.5,1.5,0,5.5 \
        interp${n}.plt
done

In the finite-difference grid, a Gaussian filter can be easily applied by convolution operation to remove small scale vortices. Figure 3 shows that with decreasing filter size, there are more and more small scale vortices in the Q iso-surface.

Figure 3. Q iso-surface coloured by the spanwise vorticity. Post-processed in a finite-difference grid. sigma is the standard deviation of the Gaussian filter. (a) sigma = 0.1. (b) sigma=0.07. (c) sigma=0.05. (d) unfiltered, the same as figure 2.

The same operation can also be applied to 2D and 3DH1D fields. The finite different tool is a small c++ code available here https://github.com/gaoak/ptspostprocessing