DOI: 10.2139/ssrn.4632754
We present NekMesh: an open-source mesh generation package which is designed to enable the generation of valid, high-quality curvilinear meshes of complex, three-dimensional geometries for performing high-order simulations.
DOI: 10.1017/jfm.2023.735
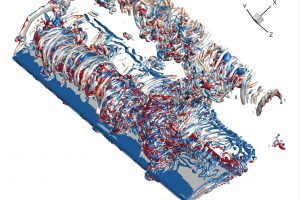
The three-dimensional (3-D) transition of the leading-edge vortex (LEV) and the force characteristics of the plunging airfoil are investigated in the chord-based Strouhal number Stc range of 0.10 to 1.0 by means of experimental measurements, numerical simulations and linear stability analysis in order to understand the spanwise instabilities and the
effects on the force.
DOI: 10.2514/6.2023-3831
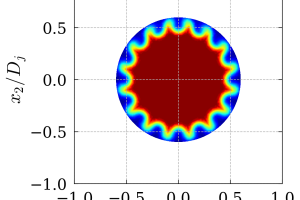
Large Eddy Simulations (LES) in combination with the Ffowcs Williams – Hawkings method to study the influence of chevrons on the flow field as well as the noise produced by a closely installed M = 0.6 jet.
DOI: 10.1007/s10494-023-00404-7
A computational study of a multi-element aerofoil containing unsteady analysis of force and surface pressure data. The mainplane and flap laminar separation are studied and the cross-spectral phase is presented for the lower frequency modes.
DOI: 10.2514/6.2023-1546
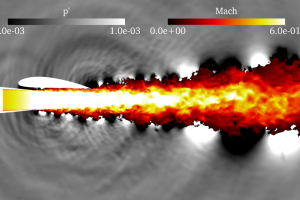
A recently developed computational framework for jet noise is used to compute the noise generated by an isolated and installed jet.
Development of two fluid-structure interaction (FSI) solvers for simulations of highly deformable nonlinear slender structures.
DOI: 10.1017/jfm.2022.224
The vortex dynamics of leading-edge vortices on plunging high-aspect-ratio (AR = 10)
wings and airfoils were investigated by means of volumetric velocity measurements,
numerical simulations and stability analysis to understand the deformation of the
leading-edge vortex filament and spanwise instabilities.
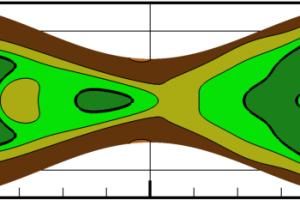
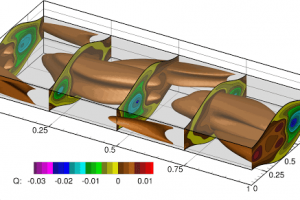
Can hydrodynamic instability be used for mixing? And at the same time can conduits be shaped such that hydraulic losses are reduced? We think that it is Yes to both.
Nektar++ has been used to study various forms of hydrodynamic instabilities arising is a flow through a channel with corrugated walls. Stability analysis has been performed using direct numerical simulation and tracking growth, or attenuation of the unstable modes.
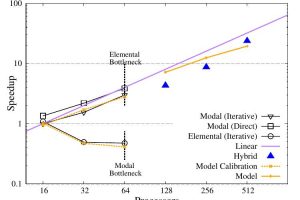
An adaptable parallel algorithm for the direct numerical simulation of incompressible turbulent flows using a Fourier spectral/hp element method and MPI virtual topologies
DOI: 10.1016/j.cpc.2016.04.011
Abstract: A hybrid parallelisation technique for distributed memory systems is investigated for a coupled Fourier-spectral/hp element discretisation of domains characterised by geometric homogeneity in one or more directions.