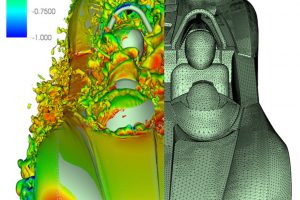
We present the successful deployment of high-fidelity Large-Eddy Simulation (LES) technologies based on spectral/hp element methods (SEM) to an industry-relevant configuration. The simulation is carried out on a real automotive car, namely the Elemental Rp1 model.

Nektar++ has been recently used to verify the dispersion/diffusion estimates of discontinuous spectral element methods for non-periodic flow problems. This work a key implications on the effective construction of LES tools for industrial problems.

The ECMWF HPC facilities are composed by two identical Cray XC30 systems that support both operational forecast requirements of the centre and research.

Copper is a Cray XE6 system and supports research programs of the United the States Department of Defense (DoD). The system is provided for computationally based science and engineering and is intended for high performance computing, large-scale storage, and utility computing.

DOI: 10.1007/s10915-015-0119-z/fulltext.html
This paper investigates the connections between many popular variants of the well-established discontinuous Galerkin method and the recently developed high-order flux reconstruction approach on irregular tensor-product grids.

DOI: 10.1016/j.jcp.2015.06.032
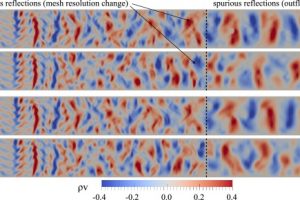
In this work we detail two dealiasing strategies based on the concept of consistent integration. The first uses a localised approach, which is useful when the nonlinearities only arise in parts of the problem. The second is based on the more traditional approach of using a higher quadrature.

DOI: 10.1017/jfm.2015.281
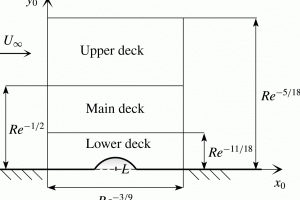
This paper is concerned with the boundary-layer separation in subsonic and transonic flows caused by a two-dimensional isolated wall roughness. The process of the separation is analysed by means of two approaches: the direct numerical simulation (DNS) of the flow using the Navier–Stokes equations, and the numerical solution of the triple-deck equations.

DOI: 10.2514/6.2014-2923
The nature of boundary conditions, and how they are implemented, can have a significant impact on the stability and accuracy of a Computational Fluid Dynamics (CFD) solver. The objective of this paper is to assess how different boundary conditions impact the performance of compact discontinuous high-order spectral element methods (such as the discontinuous Galerkin method and the Flux Reconstruction approach), when these schemes are used to solve the Euler and compressible Navier-Stokes equations on unstructured grids.