DOI: 10.1007/s10915-015-0119-z/fulltext.html
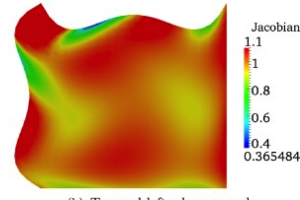
This paper investigates the connections between many popular variants of the well-established discontinuous Galerkin method and the recently developed high-order flux reconstruction approach on irregular tensor-product grids.

DOI: 10.1016/j.jcp.2015.06.032
In this work we detail two dealiasing strategies based on the concept of consistent integration. The first uses a localised approach, which is useful when the nonlinearities only arise in parts of the problem. The second is based on the more traditional approach of using a higher quadrature.

DOI: 10.1016/j.jcp.2015.06.020
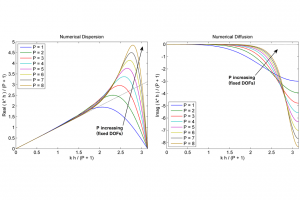
We investigate the potential of linear dispersion–diffusion analysis in providing direct guidelines for turbulence simulations through the under-resolved DNS (sometimes called implicit LES) approach via spectral/hp methods. The discontinuous Galerkin (DG) formulation is assessed in particular as a representative of these methods.