Linear dispersion-diusion analysis and its application to under-resolved turbulence simulations using discontinuous Galerkin spectral/hp methods
DOI: http://dx.doi.org/10.1016/j.jcp.2015.06.020
Abstract (illustrated):
We investigate the potential of linear dispersion–diffusion analysis in providing direct guidelines for turbulence simulations through the under-resolved DNS (sometimes called implicit LES) approach via spectral/hp methods. The discontinuous Galerkin (DG) formulation is assessed in particular as a representative of these methods. We revisit the eigensolutions technique as applied to linear advection and suggest a new perspective to the role of multiple numerical modes, peculiar to spectral/hp methods.
Multiple eigenmodes for linear advection with P = 2
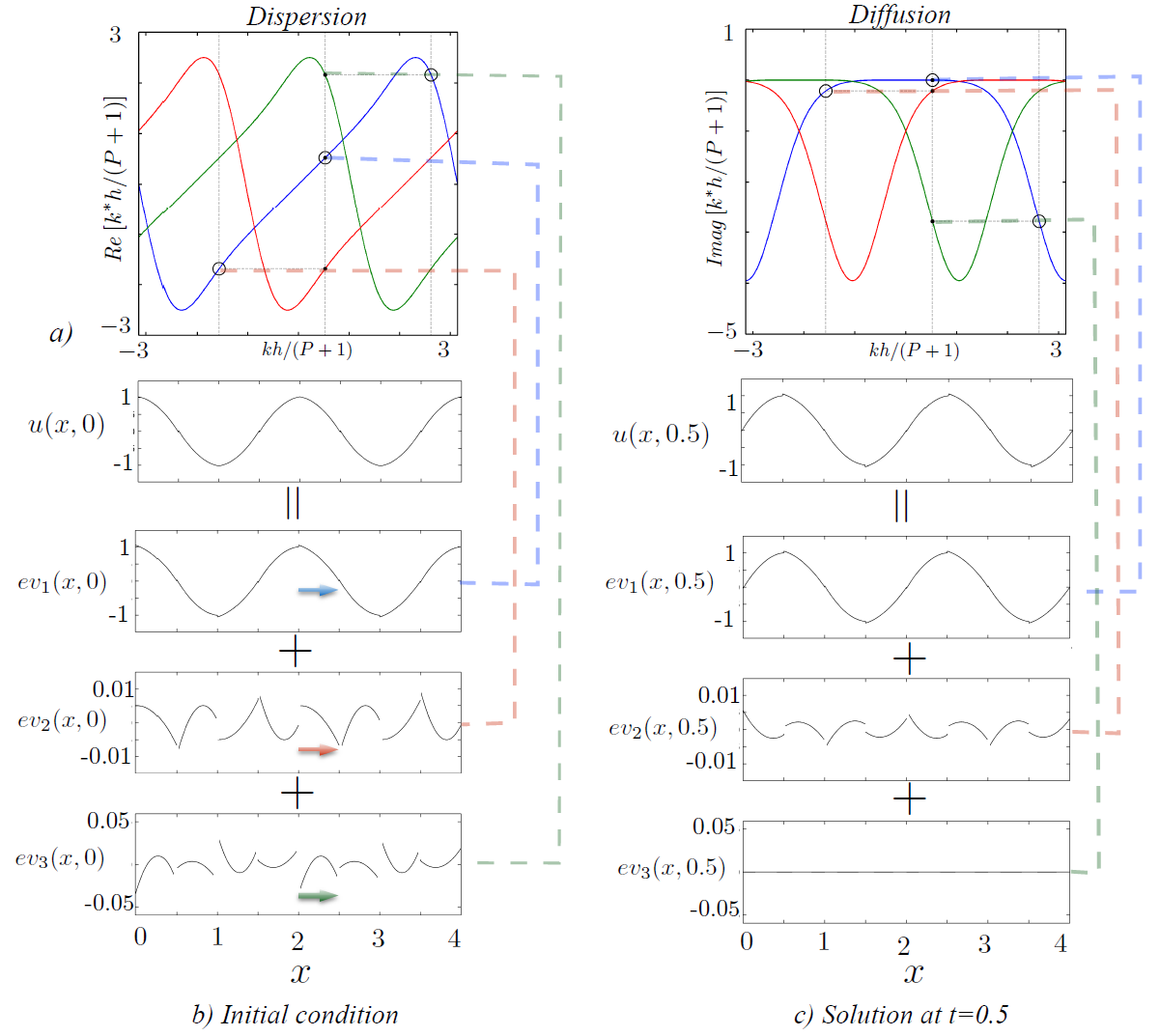
From this new perspective, “secondary” eigenmodes are seen to replicate the propagation behaviour of a “primary” mode, so that DG’s propagation characteristics can be obtained directly from the dispersion–diffusion curves of the primary mode. Numerical dissipation is then appraised from these primary eigencurves and its effect over poorly-resolved scales is quantified. Within this scenario, a simple criterion is proposed to estimate DG’s effective resolution in terms of the largest wavenumber it can accurately resolve in a given hp approximation space, also allowing us to present points per wavelength estimates typically used in spectral and finite difference methods.
Effective resolution power on (forced) Burgers turbulence
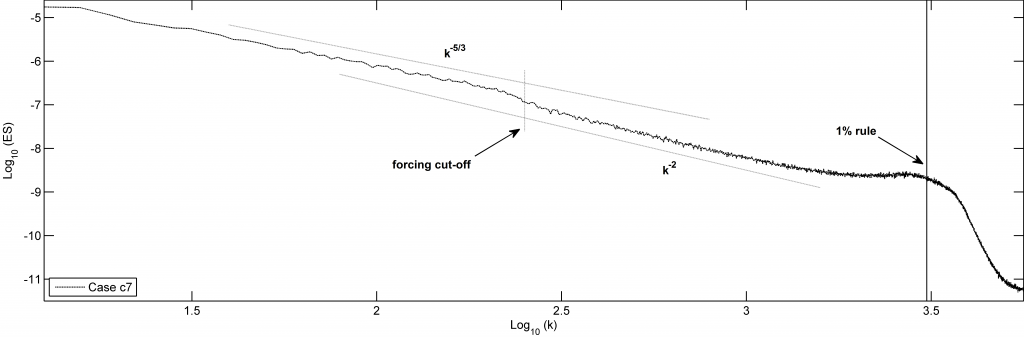
Although strictly valid for linear advection, the devised criterion is tested against (1D) Burgers turbulence and found to predict with good accuracy the beginning of the dissipation range on the energy spectra of under-resolved simulations. The analysis of these test cases through the proposed methodology clarifies why and how the DG formulation can be used for under-resolved turbulence simulations without explicit subgrid-scale modelling.
Increase in resolution power with P, for a fixed number of DOFs
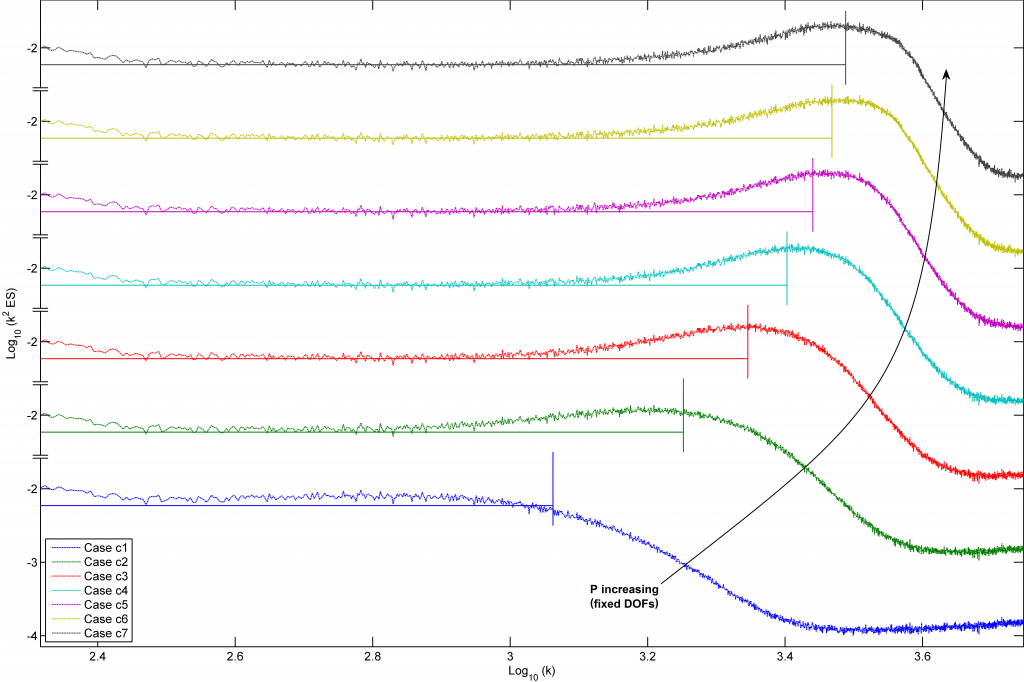
In particular, when dealing with communication limited hardware which forces one to consider the performance for a fixed number of degrees of freedom, the use of higher polynomial orders along with moderately coarser meshes is shown to be the best way to translate available degrees of freedom into resolution power.
Comparing same-DOF solutions: P = 1 on fine mesh (left) vs. P = 7 on coarse mesh (right)