Performe force diagnostics in Nektar++
Hydrodynamic force exhibits close correlations with flow structures. For example, a low-pressure regime is often observed when a concentrated vortex exists near the wall. A series of diagnostic methods has been developed in the past decades to elucidate these relationships. We have implemented the diagnostic method developed by Gao et al. (2019a, 2019b, 2025) as FieldConvert modules in Nektar++ to provide convenience for pressure force analysis.
The method is based on the governing equation and boundary conditions of the pressure field. First, in incompressible flow with a constant density, the pressure Poisson equation is
The Neumann boundary condition for the pressure is
Here, is the velocity field of the flow; is the constant density of the flow; is the second invariant of the velocity gradient tensor, ; is the unit normal vector of the boundary pointing from the solid side to the fluid side; is the acceleration of the fluid particle on the boundary; is the dynamic viscosity of the fluid. For viscous flow, the acceleration of the fluid particle equals that of the solid particle due to the no-slip boundary condition.
The above equations show that the pressure force depends on three factors: the flow structures characterised by , the wall-normal acceleration, and the viscous effect in the pressure boundary condition. To quantify influences from these factors, the adjoint equation of the pressure Poisson equation is introduced
with Neumann boundary condition
measures the sensitivity of the weighted pressure force to these nonhomogeneous terms, and the weighted pressure force can be decomposed into three components
The three terms on the right-hand side are termed flow structure-induced force (or -induced force for brevity), the wall-acceleration force, and the viscous pressure force. The corresponding integrands also present sensitivity of the weighted pressure force to the local volume or surface force elements.
The following issues should be noted. First, it is inappropriate to call the -induced force “the vortex-induced force”, since both positive and negative contribute to the integraion; while the negative represents flow structures dominated by strain rate, instead of rotation. As illustrated in the literature, a vortical structure, , generates a suction force on the solid surface, whereas a strain-rate structure, , creates a repulsive force on the solid surface. Second, the wall-acceleration force is not equivalent to the added-mass force of the potential flow. Only for a rigid body with translational motion, the wall-acceleration force equals the added-mass force; generally, they are different.
To perform the above analysis, the adjoint field should first be calculated using the ADRSolver. Then, the FieldConvert modules can be called correspondingly. mpirun -np 8 ADRSolver mesh.xml phi.xml -v
FieldConvert -m QCriterion mesh.xml NS.xml field.chk Q.fld -f
FieldConvert mesh.xml Q.fld mesh.fld combine.fld -f
FieldConvert -f -v -m FDecomposeBnd mesh.xml NS.xml combine.fld stdout > bndlog
FieldConvert -f -v -m FDecomposeVol:box=-3,6,-3,3,0,0:scandir=0 mesh.xml NS.xml combine.fld combine.plt > vollog
Here, this feature is tested in the 2D flow past a circular cylinder at Re=800, see below.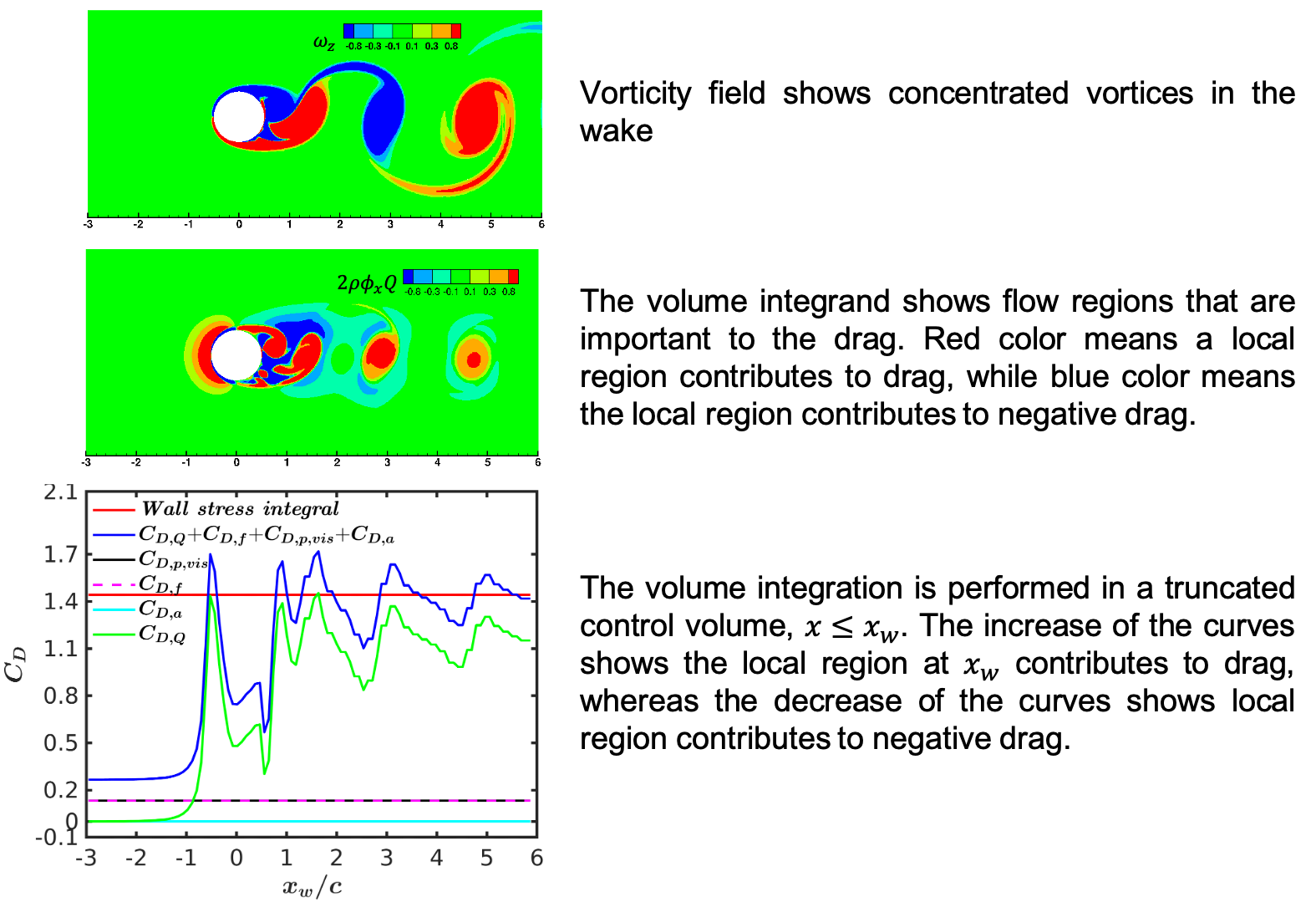
The top figure shows the vorticity field. The middle figure shows the volume integrand for the drag, . The bottom figure shows the dependence of the volume integration over the control volume: .
References
Gao, A.-K., Zou, S.-F., Shi, Y.-P. & Wu, J.-Z. 2019a Passing-over leading-edge vortex: the thrust booster in heaving airfoil. AIP Adv. 9 (3), 035314.10.1063/1.5064696
Gao, A.-K. & Wu, J.-Z. 2019b A note on the Galilean invariance of aerodynamic force theories in unsteady incompressible flows. Acta Mech. Sinica 35, 1150–1154.
Gao, A.-K., Xie, C.-Y. & Lu, X.-Y. 2025 Weighted integral methods for fluid force diagnostics in incompressible flows. J. Fluid Mech. 1024, A57.10.1017/jfm.2025.10854