DOI: http://dx.doi.org/10.1016/j.jcp.2015.12.009

Abstract (illustrated):

This study addresses linear dispersion–diffusion analysis for the spectral/hp continuous Galerkin (CG) formulation in one dimension. First, numerical dispersion and diffusion curves are obtained for the advection–diffusion problem and the role of multiple eigencurves peculiar to spectral/hp methods is discussed. From the eigencurves’ behaviour, we observe that CG might feature potentially undesirable non-smooth dispersion/diffusion characteristics for under-resolved simulations of problems strongly dominated by either convection or diffusion.

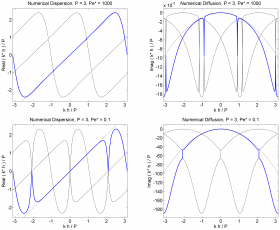
Potentially undesirable dispersion–diffusion behaviour observed for CG (very high or very small Peclet numbers)

Subsequently, the linear advection equation augmented with spectral vanishing viscosity (SVV) is analysed. Dispersion and diffusion characteristics of CG with SVV-based stabilization are verified to display similar non-smooth features in flow regions where convection is much stronger than dissipation or vice-versa, owing to a dependency of the standard SVV operator on a local Péclet number. First a modification is proposed to the traditional SVV scaling that enforces a globally constant Péclet number so as to avoid the previous issues. In addition, a new SVV kernel function is suggested and shown to provide a more regular behaviour for the eigencurves along with a consistent increase in resolution power for higher-order discretizations, as measured by the extent of the wavenumber range where numerical errors are negligible.

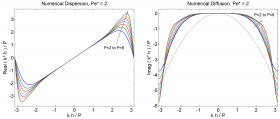
Well-behaved eigencurves through the modified SVV operator (which holds Peclet fixed)

The dissipation characteristics of CG with the SVV modifications suggested are then verified to be broadly equivalent to those obtained through upwinding in the discontinuous Galerkin (DG) scheme. Nevertheless, for the kernel function proposed, the full upwind DG scheme is found to have a slightly higher resolution power for the same dissipation levels. These results show that improved CG-SVV characteristics can be pursued via different kernel functions with the aid of optimization algorithms.

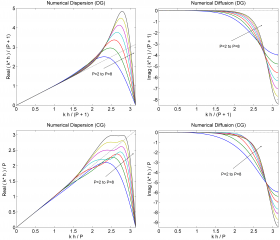
Comparing DG (top) with optimized CG+SVV (bottom)