|
Defines |
| #define | zwgl(z, w, np) zwgj (z,w,np,0.0,0.0); |
| #define | zwgrlm(z, w, np) zwgrjm(z,w,np,0.0,0.0); |
| #define | zwgrlp(z, w, np) zwgrjp(z,w,np,0.0,0.0); |
| #define | zwgll(z, w, np) zwglj (z,w,np,0.0,0.0); |
| #define | zwgc(z, w, np) zwgj (z,w,np,-0.5,-0.5); |
| #define | zwgrcm(z, w, np) zwgrjm(z,w,np,-0.5,-0.5); |
| #define | zwgrcp(z, w, np) zwgrjp(z,w,np,-0.5,-0.5); |
| #define | zwglc(z, w, np) zwglj (z,w,np,-0.5,-0.5); |
| #define | Dgl(d, dt, z, np) Dgj (*d,*dt,z,np,0.0,0.0); |
| #define | Dgrlm(d, dt, z, np) Dgrjm(*d,*dt,z,np,0.0,0.0); |
| #define | Dgrlp(d, dt, z, np) Dgrjp(*d,*dt,z,np,0.0,0.0); |
| #define | Dgll(d, dt, z, np) Dglj (*d,*dt,z,np,0.0,0.0); |
| #define | Dgc(d, dt, z, np) Dgj (*d,*dt,z,np,-0.5,-0.5); |
| #define | Dgrcm(d, dt, z, np) Dgrjm(*d,*dt,z,np,-0.5,-0.5); |
| #define | Dgrcp(d, dt, z, np) Dgrjp(*d,*dt,z,np,-0.5,-0.5); |
| #define | Dglc(d, dt, z, np) Dglj (*d,*dt,z,np,-0.5,-0.5); |
| #define | hgl(i, z, zgj,np) hgj ( i,z,zgj ,np,0.0,0.0); |
| #define | hgrlm(i, z, zgrj, np) hgrjm(i,z,zgrj,np,0.0,0.0); |
| #define | hgrlp(i, z, zgrj, np) hgrjp(i,z,zgrj,np,0.0,0.0); |
| #define | hgll(i, z, zglj, np) hglj (i,z,zglj,np,0.0,0.0); |
| #define | hgc(i, z, zgj,np) hgj( i,z,zgj ,np,-0.5,-0.5); |
| #define | hgrc(i, z, zgrj, np) hgrjm(i,z,zgrj,np,-0.5,-0.5); |
| #define | hglc(i, z, zglj, np) hglj( i,z,zglj,np,-0.5,-0.5); |
| #define | Imgl(im, zgl,zm, nz, mz) Imgj (im,zgl ,zm,nz,mz,0.0,0.0) |
| #define | Imgrlm(im, zgrl, zm, nz, mz) Imgrjm(im,zgrl,zm,nz,mz,0.0,0.0) |
| #define | Imgrlp(im, zgrl, zm, nz, mz) Imgrjp(im,zgrl,zm,nz,mz,0.0,0.0) |
| #define | Imgll(im, zgll, zm, nz, mz) Imglj (im,zgll,zm,nz,mz,0.0,0.0) |
| #define | Imgc(im, zgl,zm, nz, mz) Imgj (im,zgl ,zm,nz,mz,-0.5,-0.5) |
| #define | Imgrcm(im, zgrl, zm, nz, mz) Imgrjm(im,zgrl,zm,nz,mz,-0.5,-0.5) |
| #define | Imgrcp(im, zgrl, zm, nz, mz) Imgrjp(im,zgrl,zm,nz,mz,-0.5,-0.5) |
| #define | Imglc(im, zgll, zm, nz, mz) Imglj (im,zgll,zm,nz,mz,-0.5,-0.5) |
| #define | zwgrj(z, w, np, alpha, beta) zwgrjm (z,w,np,alpha,beta) |
| #define | zwgrl(z, w, np) zwgrjm (z,w,np,0.0,0.0); |
| #define | hgrj(i, z, zgrj, np, alpha, beta) hgrjm (i,z,zgrj,np,alpha,beta) |
| #define | hgrl(i, z, zgrj, np) hgrjm(i,z,zgrj,np,0.0,0.0); |
| #define | jacobf(np, z, p,n, alpha, beta) jacobfd(np,z,p,NULL ,n,alpha,beta) |
| #define | igjm(im, zgl, zm, nz, mz, alpha, beta) Imgj (*im,zgl ,zm,nz,mz,alpha,beta) |
| #define | igrjm(im, zgrl, zm, nz, mz, alpha, beta) Imgrjm(*im,zgrl,zm,nz,mz,alpha,beta) |
| #define | igljm(im, zgll, zm, nz, mz, alpha, beta) Imglj (*im,zgll,zm,nz,mz,alpha,beta) |
| #define | iglm(im, zgl,zm, nz, mz) Imgj (*im,zgl ,zm,nz,mz,0.0,0.0) |
| #define | igrlm(im, zgrl, zm, nz, mz) Imgrjm(*im,zgrl,zm,nz,mz,0.0,0.0) |
| #define | igllm(im, zgll, zm, nz, mz) Imglj (*im,zgll,zm,nz,mz,0.0,0.0) |
| #define | dgj(d, dt, z, np, alpha, beta) Dgj (*d,*dt,z,np,alpha,beta) |
| #define | dgrj(d, dt, z, np, alpha, beta) Dgrjm(*d,*dt,z,np,alpha,beta) |
| #define | dglj(d, dt, z, np, alpha, beta) Dglj (*d,*dt,z,np,alpha,beta) |
| #define | dgll(d, dt, z, np) Dglj (*d,*dt,z,np,0.0,0.0); |
| #define | dgrl(d, dt, z, np) Dgrjm(*d,*dt,z,np,0.0,0.0); |
Functions |
| void | zwgj (double *, double *, int, double, double) |
| | Gauss-Jacobi zeros and weights.
|
| void | zwgrjm (double *, double *, int, double, double) |
| | Gauss-Radau-Jacobi zeros and weights with end point at z=-1.
|
| void | zwgrjp (double *, double *, int, double, double) |
| | Gauss-Radau-Jacobi zeros and weights with end point at z=1.
|
| void | zwglj (double *, double *, int, double, double) |
| | Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1.
|
| void | Dgj (double *, double *, double *, int, double, double) |
| | Compute the Derivative Matrix and its transpose associated with the Gauss-Jacobi zeros.
|
| void | Dgrjm (double *, double *, double *, int, double, double) |
| | Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=-1.
|
| void | Dgrjp (double *, double *, double *, int, double, double) |
| | Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=1.
|
| void | Dglj (double *, double *, double *, int, double, double) |
| | Compute the Derivative Matrix and its transpose associated with the Gauss-Lobatto-Jacobi zeros.
|
| double | hgj (int, double, double *, int, double, double) |
| | Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi points zgj at the arbitrary location z.
|
| double | hgrjm (int, double, double *, int, double, double) |
| | Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point -1.
|
| double | hgrjp (int, double, double *, int, double, double) |
| | Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point +1.
|
| double | hglj (int, double, double *, int, double, double) |
| | Compute the value of the i th Lagrangian interpolant through the np Gauss-Lobatto-Jacobi points zgrj at the arbitrary location z.
|
| void | Imgj (double *, double *, double *, int, int, double, double) |
| | Interpolation Operator from Gauss-Jacobi points to an arbitrary distrubtion at points zm.
|
| void | Imgrjm (double *, double *, double *, int, int, double, double) |
| | Interpolation Operator from Gauss-Radau-Jacobi points (including z=-1) to an arbitrary distrubtion at points zm.
|
| void | Imgrjp (double *, double *, double *, int, int, double, double) |
| | Interpolation Operator from Gauss-Radau-Jacobi points (including z=1) to an arbitrary distrubtion at points zm.
|
| void | Imglj (double *, double *, double *, int, int, double, double) |
| | Interpolation Operator from Gauss-Lobatto-Jacobi points to an arbitrary distrubtion at points zm.
|
| void | jacobfd (int, double *, double *, double *, int, double, double) |
| | Routine to calculate Jacobi polynomials, 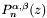 , and their first derivative, , and their first derivative, 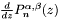 . .
|
| void | jacobd (int, double *, double *, int, double, double) |
| | Calculate the derivative of Jacobi polynomials.
|
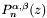 , and their first derivative,
, and their first derivative, 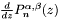 .
. 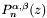 , and their first derivative,
, and their first derivative, 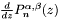 .
.  1.3
1.3