Defines
Functions
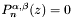 .
. 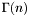 , for integer values and halves.
, for integer values and halves. 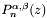 , and their first derivative,
, and their first derivative, 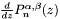 .
. #include <stdlib.h>#include <sys/types.h>#include <stdio.h>#include <float.h>#include <math.h>#include "polylib.h"Go to the source code of this file.
Defines | |
| #define | STOP 30 |
| #define | EPS 100*DBL_EPSILON |
| #define | sign(a, b) ((b)<0 ? -fabs(a) : fabs(a)) |
| #define | jacobz(n, z, alpha, beta) JacZeros(n,z,alpha,beta) |
| zero determination using eigenvalues of tridiagaonl matrix | |
Functions | |
| void | Jacobz (int n, double *z, double alpha, double beta) |
Calculate the n zeros, z, of the Jacobi polynomial, i.e. 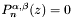 . . | |
| void | JacZeros (int n, double *a, double alpha, double beta) |
| Zero determination through the eigenvalues of a tridiagonal matrix from teh three term recursion relationship. | |
| void | TriQL (int n, double *d, double *e) |
| QL algorithm for symmetric tridiagonal matrix. | |
| double | gammaF (double) |
Calculate the Gamma function , 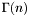 , for integer values and halves. , for integer values and halves. | |
| void | zwgj (double *z, double *w, int np, double alpha, double beta) |
| Gauss-Jacobi zeros and weights. | |
| void | zwgrjm (double *z, double *w, int np, double alpha, double beta) |
| Gauss-Radau-Jacobi zeros and weights with end point at z=-1. | |
| void | zwgrjp (double *z, double *w, int np, double alpha, double beta) |
| Gauss-Radau-Jacobi zeros and weights with end point at z=1. | |
| void | zwglj (double *z, double *w, int np, double alpha, double beta) |
| Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1. | |
| void | Dgj (double *D, double *Dt, double *z, int np, double alpha, double beta) |
| Compute the Derivative Matrix and its transpose associated with the Gauss-Jacobi zeros. | |
| void | Dgrjm (double *D, double *Dt, double *z, int np, double alpha, double beta) |
| Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=-1. | |
| void | Dgrjp (double *D, double *Dt, double *z, int np, double alpha, double beta) |
| Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=1. | |
| void | Dglj (double *D, double *Dt, double *z, int np, double alpha, double beta) |
| Compute the Derivative Matrix and its transpose associated with the Gauss-Lobatto-Jacobi zeros. | |
| double | hgj (int i, double z, double *zgj, int np, double alpha, double beta) |
| Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi points zgj at the arbitrary location z. | |
| double | hgrjm (int i, double z, double *zgrj, int np, double alpha, double beta) |
| Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point -1. | |
| double | hgrjp (int i, double z, double *zgrj, int np, double alpha, double beta) |
| Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point +1. | |
| double | hglj (int i, double z, double *zglj, int np, double alpha, double beta) |
| Compute the value of the i th Lagrangian interpolant through the np Gauss-Lobatto-Jacobi points zgrj at the arbitrary location z. | |
| void | Imgj (double *im, double *zgj, double *zm, int nz, int mz, double alpha, double beta) |
| Interpolation Operator from Gauss-Jacobi points to an arbitrary distrubtion at points zm. | |
| void | Imgrjm (double *im, double *zgrj, double *zm, int nz, int mz, double alpha, double beta) |
| Interpolation Operator from Gauss-Radau-Jacobi points (including z=-1) to an arbitrary distrubtion at points zm. | |
| void | Imgrjp (double *im, double *zgrj, double *zm, int nz, int mz, double alpha, double beta) |
| Interpolation Operator from Gauss-Radau-Jacobi points (including z=1) to an arbitrary distrubtion at points zm. | |
| void | Imglj (double *im, double *zglj, double *zm, int nz, int mz, double alpha, double beta) |
| Interpolation Operator from Gauss-Lobatto-Jacobi points to an arbitrary distrubtion at points zm. | |
| void | jacobfd (int np, double *z, double *poly_in, double *polyd, int n, double alpha, double beta) |
Routine to calculate Jacobi polynomials, 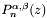 , and their first derivative, , and their first derivative, 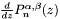 . . | |
| void | jacobd (int np, double *z, double *polyd, int n, double alpha, double beta) |
| Calculate the derivative of Jacobi polynomials. | |
|
|
Definition at line 9 of file polylib.c. Referenced by hgj(), hglj(), hgrjm(), hgrjp(), and Jacobz(). |
|
|
zero determination using eigenvalues of tridiagaonl matrix
|
|
|
Definition at line 10 of file polylib.c. Referenced by TriQL(). |
|
|
|
|
||||||||||||||||||||||||||||
|
Compute the Derivative Matrix and its transpose associated with the Gauss-Jacobi zeros.
Definition at line 321 of file polylib.c. References jacobd(). |
|
||||||||||||||||||||||||||||
|
Compute the Derivative Matrix and its transpose associated with the Gauss-Lobatto-Jacobi zeros.
|
|
||||||||||||||||||||||||||||
|
Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=-1.
|
|
||||||||||||||||||||||||||||
|
Compute the Derivative Matrix and its transpose associated with the Gauss-Radau-Jacobi zeros with a zero at z=1.
|
|
|
Calculate the Gamma function ,
Determine the value of
where Definition at line 947 of file polylib.c. Referenced by Dglj(), Dgrjm(), Dgrjp(), JacZeros(), zwgj(), zwglj(), zwgrjm(), and zwgrjp(). |
|
||||||||||||||||||||||||||||
|
Compute the value of the i th Lagrangian interpolant through the np Gauss-Jacobi points zgj at the arbitrary location z.
Definition at line 532 of file polylib.c. References EPS, jacobd(), and jacobfd(). Referenced by Imgj(). |
|
||||||||||||||||||||||||||||
|
Compute the value of the i th Lagrangian interpolant through the np Gauss-Lobatto-Jacobi points zgrj at the arbitrary location z.
Definition at line 651 of file polylib.c. References EPS, jacobd(), and jacobfd(). Referenced by Imglj(). |
|
||||||||||||||||||||||||||||
|
Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point -1.
Definition at line 569 of file polylib.c. References EPS, jacobd(), and jacobfd(). Referenced by Imgrjm(). |
|
||||||||||||||||||||||||||||
|
Compute the value of the i th Lagrangian interpolant through the np Gauss-Radau-Jacobi points zgrj at the arbitrary location z. This routine assumes zgrj includes the point +1.
Definition at line 610 of file polylib.c. References EPS, jacobd(), and jacobfd(). Referenced by Imgrjp(). |
|
||||||||||||||||||||||||||||||||
|
Interpolation Operator from Gauss-Jacobi points to an arbitrary distrubtion at points zm.
Definition at line 684 of file polylib.c. References hgj(). |
|
||||||||||||||||||||||||||||||||
|
Interpolation Operator from Gauss-Lobatto-Jacobi points to an arbitrary distrubtion at points zm.
Definition at line 766 of file polylib.c. References hglj(). |
|
||||||||||||||||||||||||||||||||
|
Interpolation Operator from Gauss-Radau-Jacobi points (including z=-1) to an arbitrary distrubtion at points zm.
Definition at line 711 of file polylib.c. References hgrjm(). |
|
||||||||||||||||||||||||||||||||
|
Interpolation Operator from Gauss-Radau-Jacobi points (including z=1) to an arbitrary distrubtion at points zm.
Definition at line 738 of file polylib.c. References hgrjp(). |
|
||||||||||||||||||||||||||||
|
Calculate the derivative of Jacobi polynomials.
Definition at line 921 of file polylib.c. References jacobfd(). Referenced by Dgj(), Dglj(), Dgrjm(), Dgrjp(), hgj(), hglj(), hgrjm(), hgrjp(), and zwgj(). |
|
||||||||||||||||||||||||||||||||
|
Routine to calculate Jacobi polynomials,
Definition at line 821 of file polylib.c. Referenced by hgj(), hglj(), hgrjm(), hgrjp(), jacobd(), Jacobz(), zwglj(), zwgrjm(), and zwgrjp(). |
|
||||||||||||||||||||
|
Calculate the n zeros, z, of the Jacobi polynomial, i.e.
This routine is only value for |
|
||||||||||||||||||||
|
Zero determination through the eigenvalues of a tridiagonal matrix from teh three term recursion relationship. Set up a symmetric tridiagonal matrix
Where the coefficients a[n], b[n] come from the recurrence relation
where |
|
||||||||||||||||
|
QL algorithm for symmetric tridiagonal matrix. This subroutine is a translation of an algol procedure, num. math. 12, 377-383(1968) by martin and wilkinson, as modified in num. math. 15, 450(1970) by dubrulle. Handbook for auto. comp., vol.ii-linear algebra, 241-248(1971). This is a modified version from numerical recipes. This subroutine finds the eigenvalues and first components of the eigenvectors of a symmetric tridiagonal matrix by the implicit QL method. on input:
on output:
Definition at line 1096 of file polylib.c. Referenced by JacZeros(). |
|
||||||||||||||||||||||||
|
Gauss-Jacobi zeros and weights.
|
|
||||||||||||||||||||||||
|
Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1.
|
|
||||||||||||||||||||||||
|
Gauss-Radau-Jacobi zeros and weights with end point at z=-1.
|
|
||||||||||||||||||||||||
|
Gauss-Radau-Jacobi zeros and weights with end point at z=1.
|
 1.3
1.3