Here
it is tried to
reproduce the convergence examples of section 2.6.2. For the first two
plots the equation was solved with as solution u(x) = sin(pi*x).
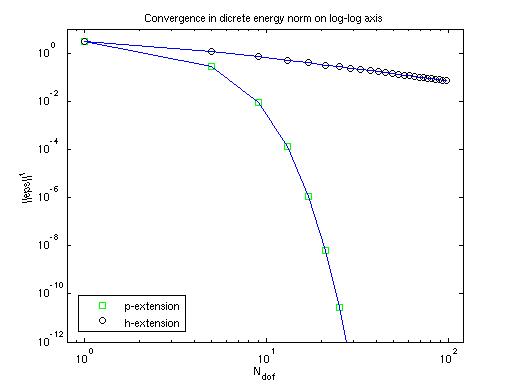
The first plot corresponds with figure 2.12(a). It can be seen that
indeed for the h-extension the line is (more or less) straight,
indicating algebraic convergence. By the way the discrete energy norm
is defined here (and in section 2.2.3 of the book) as:
Here l is the length of the
domain and
where integration is over the entire
domain. For the p-extension two elements were used and P was increased
by 4 every step (starting at 1). For the h-extension the number of
elements started at 2 and was increased by 4 every step.
The
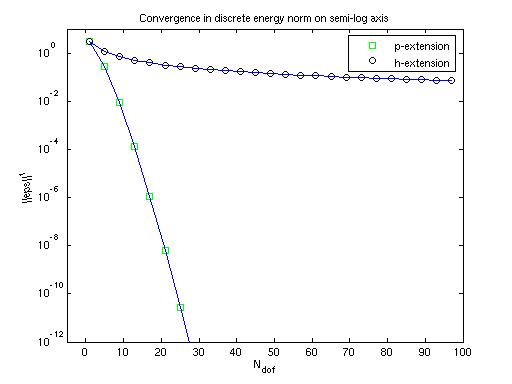
second plot
corresponds with figure 2.12(b) of the book and indeed the p-extension
line is straight, indicating exponential convergence.
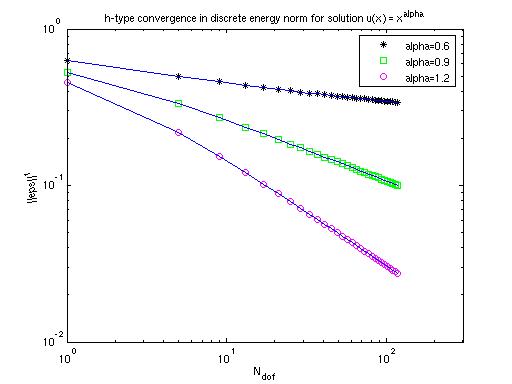
On
the third plot the
convergence can be seen for the h-extension where the solution is
non-smooth, u(x) = x^alpha. Here again P was taken 1 and
the number of elements goes in steps of four from 2 up to 97. The last
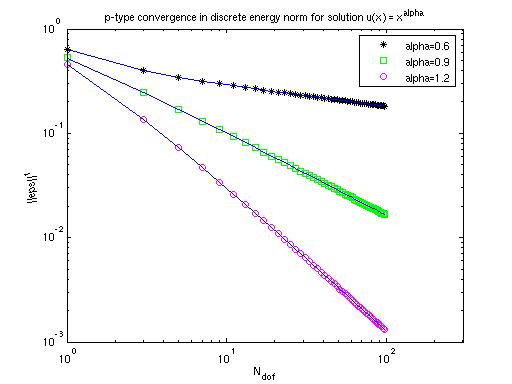
plot shows convergence to the same solution but now for the p-extension
process. Here the same orders of polynomial expansion are used as in
the first plots (and also the same number of elements namely 2). For
all figures the number of quadrature points used was twice the
polynomial order.